Understanding Gradient Descent: SSR example
As we mention in the Fitting Functions to Data blog, (Supervised) Machine Learning Algorithms are build by the following structure:
Training Function (Model)
Loss Function
Optimization
In order to optimize the loss function we have to alternatives.
Gradient Descent \(\vec{w}^{i+1} = \vec{w}^{i} - \eta \nabla L(\vec{w}^{i})\)
Simple Example
Data
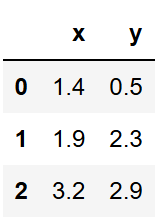
Linear Algebra notation:
\[\text{Sum of Squared Residuals (SSR)} = (\vec{y}_{\text{true}} - \vec{y}_{\text{predicted}})^t (\vec{y}_{\text{true}} - \vec{y}_{\text{predicted}})\]
Since this example has only three data points we’ll use the summation Notation
\[\text{Sum of Squared Residuals (SSR)} = \sum_{i=1}^{3} (y^i_{\text{true}} - y^i_{\text{predicted}})^2\]
Since \(y_{\text{predicted}} = w_0 + w_1\cdot x_1\) and we are assuming \(w_1\) as \(0.64\)
\[\text{Sum of Squared Residuals (SSR)} = (1.4 - w_0 + 0.64 \cdot x^1_1)^2 + (1.9 - w_0 + 0.64 \cdot x^2_1)^2 + (1.4 - w_0 + 0.64 \cdot x^3_1)^2\] \[\text{Sum of Squared Residuals (SSR)} = (1.4 - w_0 + 0.64 \cdot 0.5)^2 + (1.9 - w_0 + 0.64 \cdot 2.3)^2 + (1.4 - w_0 + 0.64 \cdot 2.9)^2\]
\[L(\vec{w}^{i}) = (1.4 - w_0 + 0.64 \cdot 0.5)^2 + (1.9 - w_0 + 0.64 \cdot 2.3)^2 + (1.4 - w_0 + 0.64 \cdot 2.9)^2\]
The derivative of our loss function
\[L(\vec{w}^{i}) = (1.4 - w_0 + 0.64 \cdot 0.5)^2 + (1.9 - w_0 + 0.64 \cdot 2.3)^2 + (1.4 - w_0 + 0.64 \cdot 2.9)^2\] Applying the chain rule
\[ \frac{\partial L(\vec{w}^{i})}{\partial w_0} = -2(1.4 - w_0 + 0.64 \cdot 0.5) -2(1.9 - w_0 + 0.64 \cdot 2.3) -2(3.2 - w_0 + 0.64 \cdot 2.9) \]
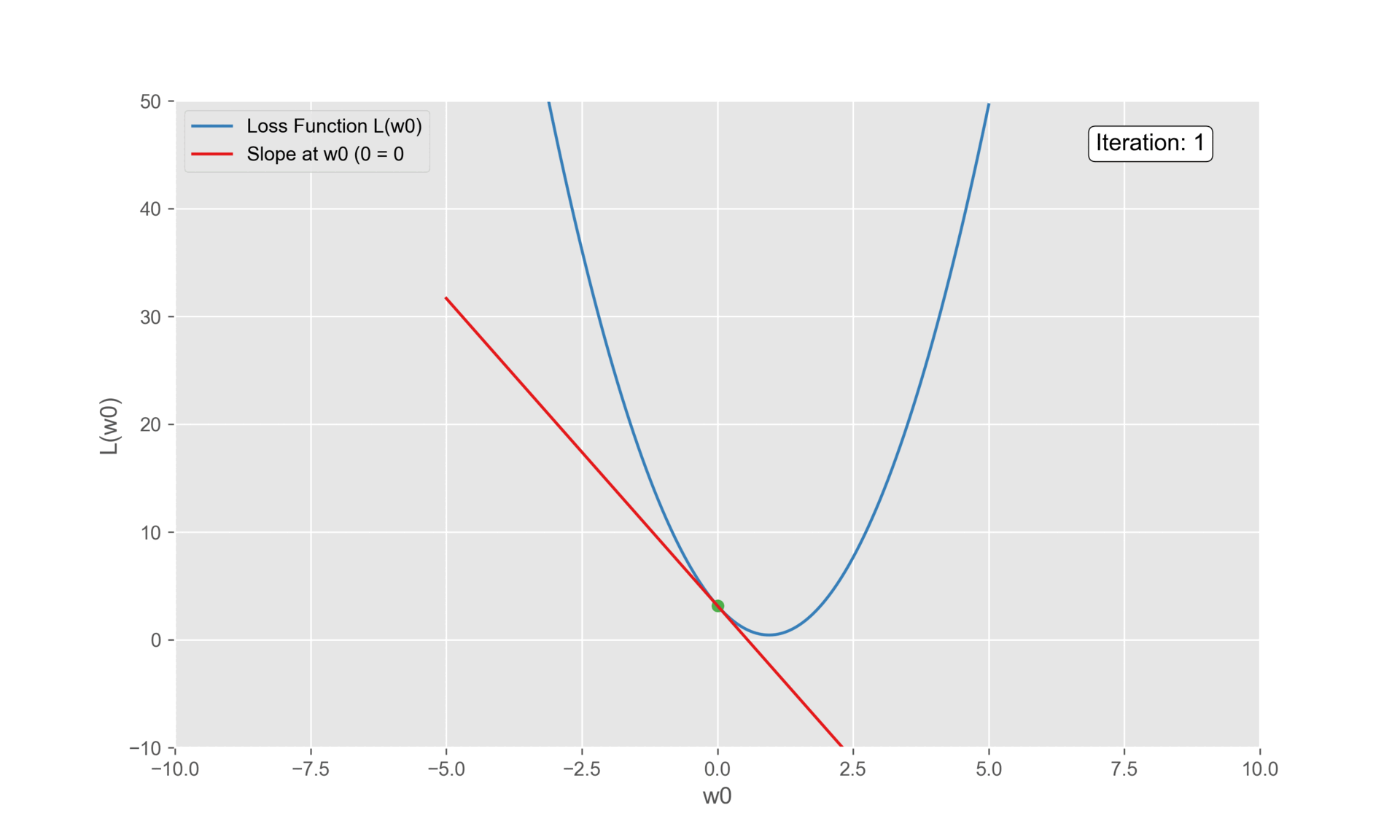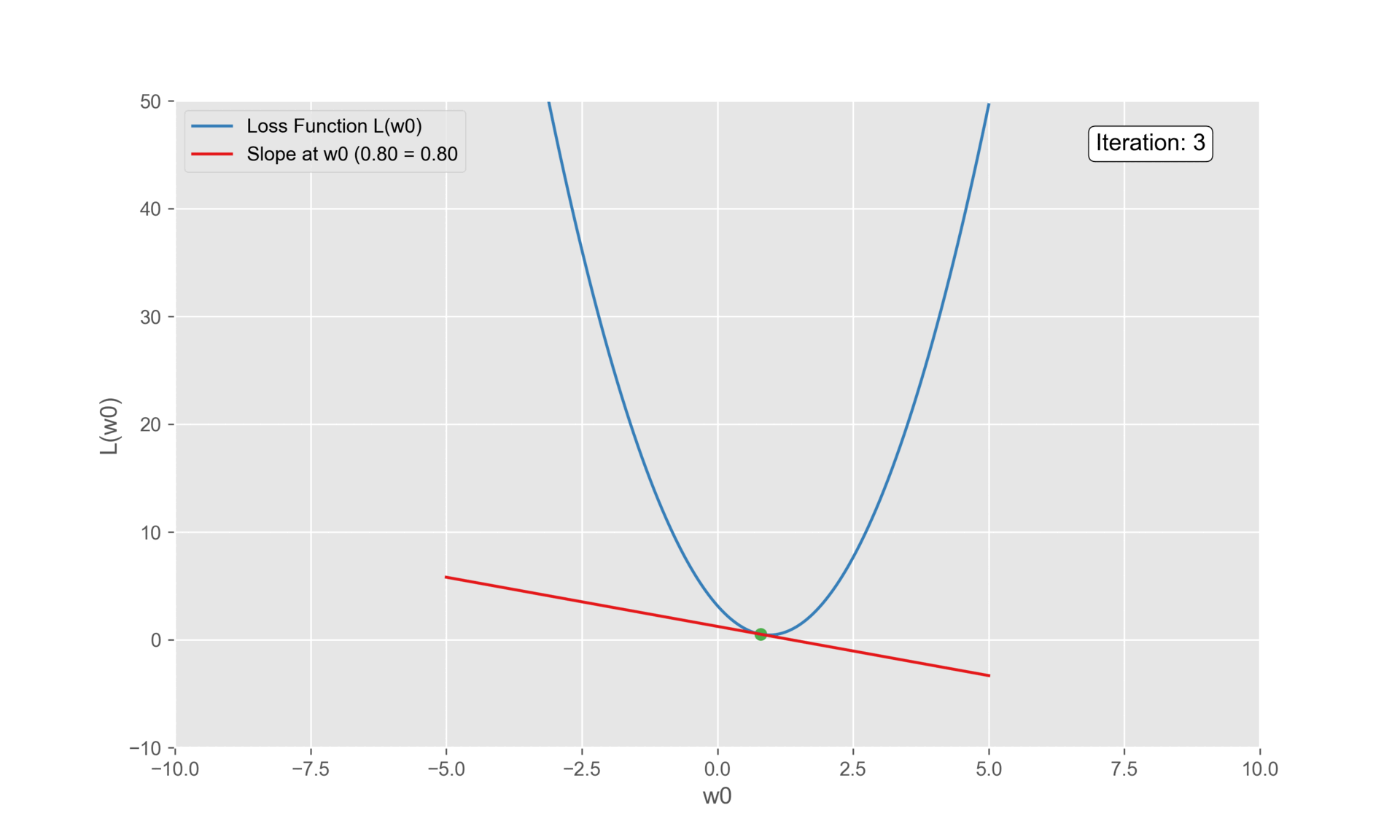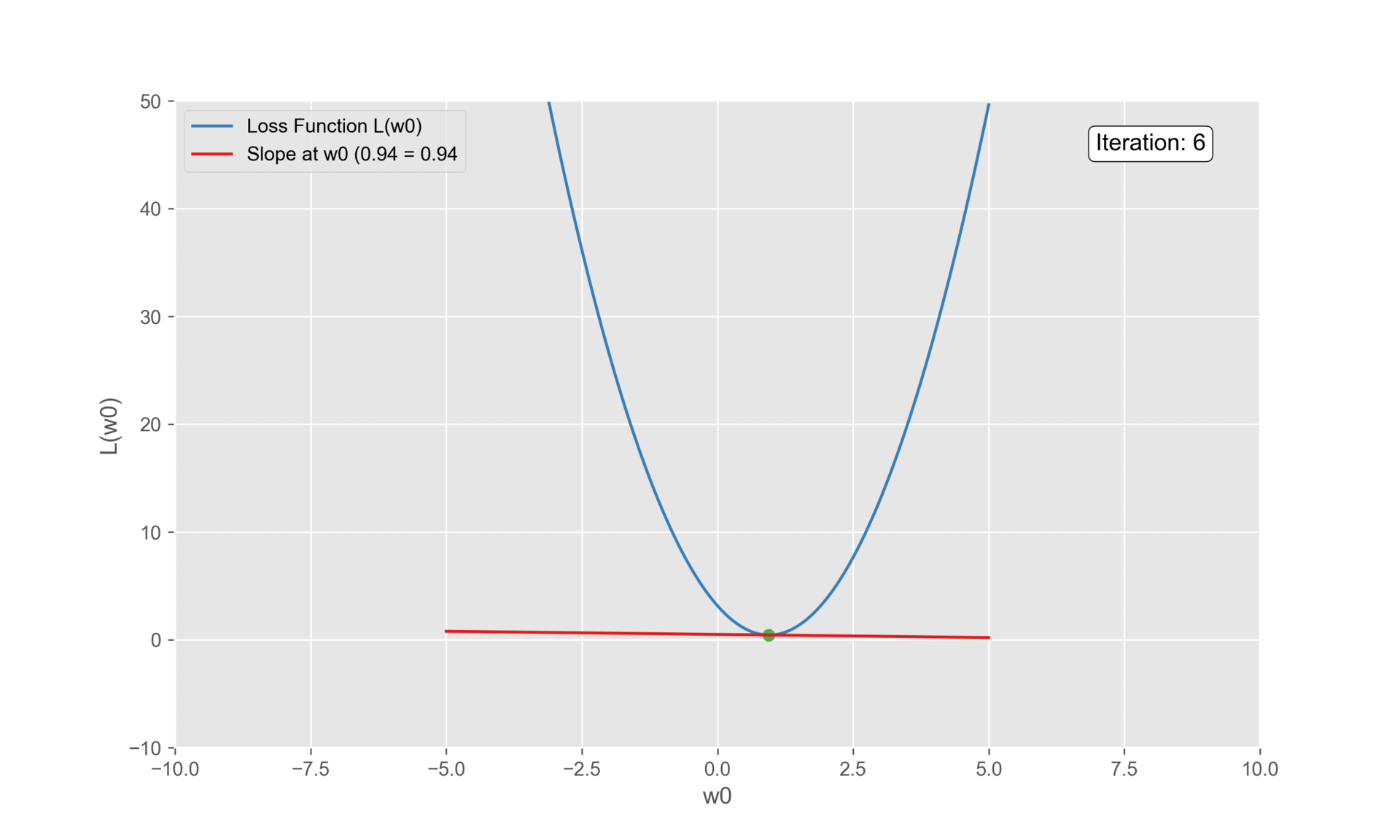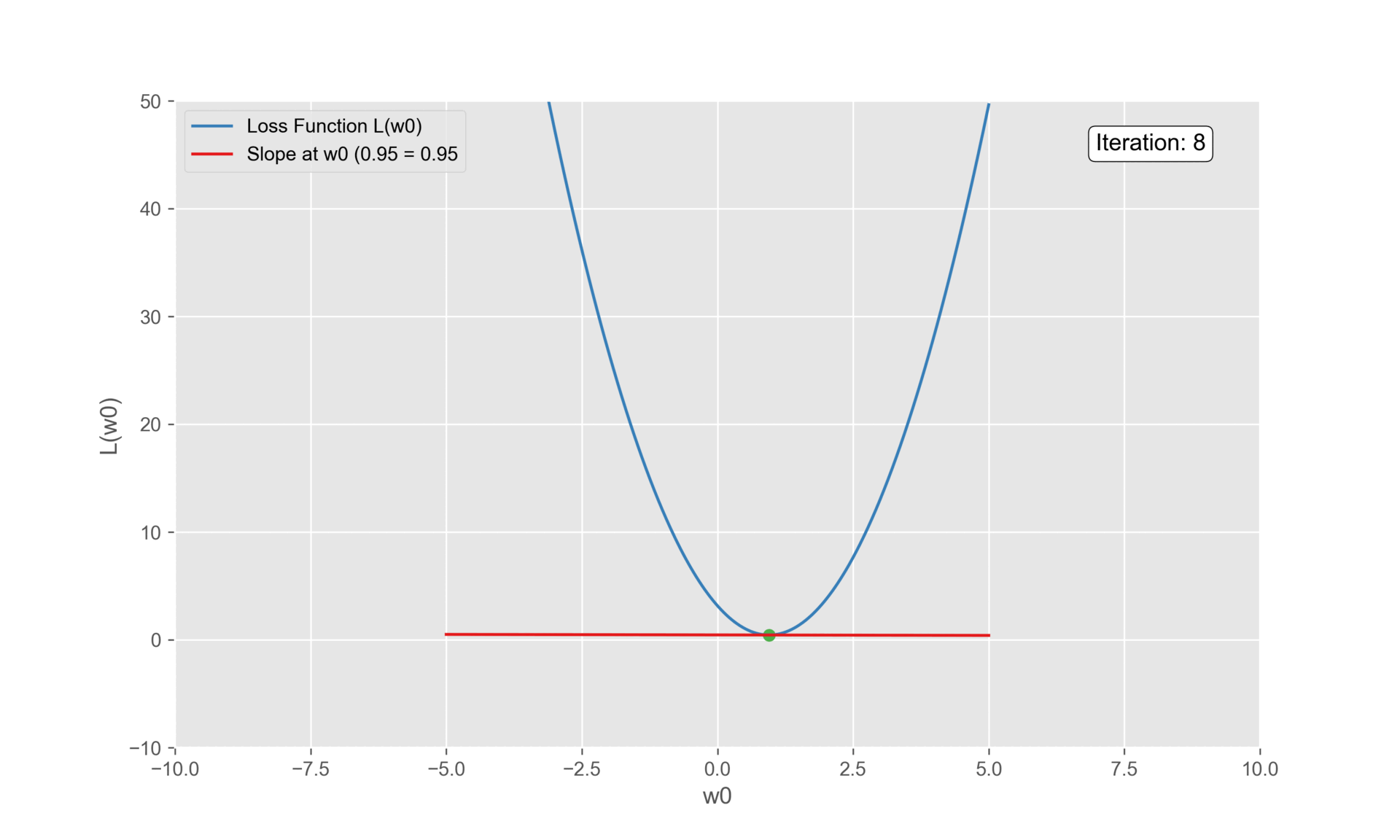
\(1^{st}\) Iteration
We need to initialize a \(w_0\) to some value.
Let’s take 0. Substituting \(w_0\) to 0:
\[\frac{\partial L(\vec{w}^{i})}{\partial w_0} = -2(1.4 - 0 + 0.64 \cdot 0.5) -2(1.9 - 0 + 0.64 \cdot 2.3) -2(1.4 - 0 + 0.64 \cdot 2.9) = -5.7\]
Calculating the step size:
\[\text{Step Size} = \eta \nabla L(\vec{w}^{i})\]
\[\text{Step Size} = 0.1 \cdot -5.7 = -0.57\]
\[w_2 =0 \cdot -(-0.57) = 0.57\]
The \(w_0\) value updates to \(0.57\).
\(2^{nd}\) Iteration
Substituting the updated value in the derivative function:
\[\frac{\partial L(\vec{w}^{i})}{\partial w_0} = -2(1.4 - 0.57 + 0.64 \cdot 0.5) -2(1.9 - 0.57 + 0.64 \cdot 2.3) -2(1.4 - 0.57 + 0.64 \cdot 2.9) = -2.3\] \[\text{Step Size} = 0.1 \cdot -2.3 = -0.23\] \[w_3 = 0.57 \cdot -(-0.23) = 0.8\]
The \(w_0\) value updates to \(0.8\).
\(3^{rd}\) Iteration
Substituting the updated value in the derivative function:
\[\frac{\partial L(\vec{w}^{i})}{\partial w_0} = -2(1.4 - 0.8 + 0.64 \cdot 0.5) -2(1.9 - 0.8 + 0.64 \cdot 2.3) -2(1.4 - 0.8 + 0.64 \cdot 2.9) = -0.9\]
\[\text{Step Size} = 0.1 \cdot -0.9 = -00.9\] \[w_4 = 0.8 \cdot -(-0.09) = 0.89\]
Acknowledgements
This blog is inspired in the you tube video Gradient Descent, Step-by-Step by StatQuest with Josh Starmer. BAM